Matched Pairs Design: Key Benefits for Statistical Studies
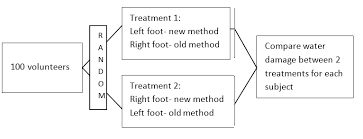
Matched pairs design is a statistical method commonly used in experimental research to increase the accuracy and precision of results. By pairing subjects based on similar characteristics and comparing outcomes within these pairs, researchers can control for variability and confounding variables, resulting in more reliable and valid findings. This design is particularly useful when random assignment is not feasible, as it allows for controlled comparisons between treatment groups, ultimately ensuring that the study’s results are both meaningful and applicable. In this comprehensive guide, we will explore the essential components of matched pairs design, its applications across various fields, and the key statistical methods used to analyze the data.
Introduction to Matched Pairs Design
Definition of Matched Pairs Design
Matched pairs design is a research methodology that involves pairing participants based on similar characteristics or measurements. The primary goal of this design is to reduce variability among groups by controlling for confounding factors, such as age, gender, or baseline health status. By ensuring that each pair is as similar as possible on key variables, researchers can more accurately assess the effect of the treatment or intervention being studied. For example, in a clinical trial evaluating a new drug, participants might be matched based on factors like age, weight, and medical history to ensure that differences in outcomes are due to the treatment rather than these confounding factors.
Matched pairs design is commonly used in experimental settings where random assignment is not possible or ethical. In clinical research, for instance, it would not be ethical to randomly assign patients with pre-existing conditions to different treatment groups without ensuring that each group is comparable. By using matched pairs design, researchers can ensure a fair comparison between groups while accounting for factors that could affect the outcome.
Historical Background
Matched pairs design has its roots in the early days of experimental research. One of the earliest uses of this design was in medical research, where it was crucial to control for individual differences in patient characteristics. By matching participants based on these variables, researchers could isolate the effect of a treatment or drug, making their conclusions more robust and generalizable. Over the years, the methodology evolved and was adapted to various fields, including psychology, education, and social sciences.
The rise of matched pairs design can be traced back to the development of statistical tools like the paired t-test, which allowed researchers to analyze the data more accurately. This design became a staple in fields like psychology and medicine, where the need for controlling individual differences was paramount. Today, matched pairs design is a fundamental part of research in multiple disciplines, ensuring that studies yield reliable and meaningful results.
Importance of Matched Pairs Design in Research
Matched pairs design plays a critical role in increasing the precision of research findings. In studies where randomization is difficult or impossible, matched pairs design offers an alternative that ensures fairer comparisons. For instance, in clinical trials, researchers often rely on matched pairs design to ensure that each participant in the treatment group is compared with someone of similar characteristics in the control group. This reduces the risk of confounding variables influencing the results, such as gender, baseline health status, or lifestyle factors.
Moreover, matched pairs design also enhances statistical power. Since variability between the pairs is minimized, it becomes easier to detect significant differences between treatment conditions. This increased sensitivity can be especially important in clinical trials where small effects may be clinically relevant. By making more efficient use of the data, matched pairs design helps researchers draw more reliable conclusions while avoiding the pitfalls of random chance.
Key Concepts and Terminology in Matched Pairs Design
Matching Process
The matching process is at the heart of matched pairs design. It involves pairing participants based on shared characteristics or baseline measurements to ensure that the two individuals in each pair are as similar as possible. Matching criteria can include demographic factors like age, gender, and socioeconomic status, or other relevant variables such as pre-treatment health conditions. For example, in a drug study, researchers may match participants who are of similar age and gender, and have comparable levels of a specific medical condition, to ensure that these variables do not skew the results.
Matching can be performed in a variety of ways, from simple one-to-one matching to more complex algorithms that account for multiple variables. The aim is to create pairs where differences between members are minimized so that any observed differences in outcomes can be attributed to the treatment or intervention being studied. Researchers must carefully consider which variables are most important for matching, as poor matching can lead to biased results.
Within-Subjects Design vs. Between-Subjects Design
Matched pairs design is often compared to within-subjects and between-subjects designs, as these are common alternatives in experimental research. In a within-subjects design, the same participants are exposed to all treatment conditions, and their responses are compared across different conditions. This design controls for individual differences because each participant serves as their own control. However, within-subjects designs may suffer from carryover effects, where participants’ experiences in one condition influence their responses in subsequent conditions.
In contrast, between-subjects designs involve comparing different groups of participants who are exposed to different conditions. While this design avoids carryover effects, it introduces the risk of variability between groups. Matched pairs design offers a middle ground by matching participants on key characteristics and comparing their outcomes across conditions, helping to control for individual differences without exposing participants to multiple treatments.
The Role of Control Groups
Control groups are essential in matched pairs design, as they provide a baseline for comparison. In a matched pairs study, each participant in the treatment group is paired with a participant in the control group, and the outcomes of these pairs are compared. The control group serves as a reference point to assess the effect of the treatment or intervention. Without a control group, it would be difficult to determine whether the observed effects were truly due to the treatment or simply the result of other factors.
Matched pairs design strengthens the role of control groups by ensuring that the treatment and control groups are as similar as possible on key characteristics. This helps to eliminate the potential for confounding variables that could affect the outcome. For example, if the control group is significantly older than the treatment group, age could influence the results. By matching participants on age, researchers can better isolate the effect of the treatment itself.
Applications of Matched Pairs Design
Use in Medical and Clinical Research
Matched pairs design is widely used in medical and clinical research to ensure the validity of study results. In clinical trials, researchers often use matched pairs to control for differences in patient characteristics that could affect treatment outcomes. For example, in a trial studying the effects of a new cancer drug, patients might be matched based on age, gender, and the stage of their illness. This ensures that the treatment group and control group are as comparable as possible, allowing researchers to more accurately assess the effectiveness of the drug.
In clinical research, matched pairs design is particularly useful when random assignment is not possible, such as in studies involving rare diseases or specific patient populations. By carefully matching patients on relevant factors, researchers can reduce the impact of confounding variables, making it easier to draw conclusions about the treatment’s efficacy. This approach has been used in a wide range of medical studies, from drug trials to surgical interventions.
Applications in Educational Research
In educational research, matched pairs design is frequently used to assess the impact of different teaching methods or interventions on student performance. For example, researchers might match students based on their baseline test scores, and then compare the performance of those who received a new teaching method with those who followed a traditional curriculum. By controlling for prior academic performance, matched pairs design ensures that differences in learning outcomes are attributable to the teaching method rather than pre-existing student differences.
Matched pairs design is also used in educational psychology to examine the effects of behavioral interventions. For instance, researchers may match students with similar behavior issues and then compare the effectiveness of different behavioral management strategies. This approach helps to control for individual differences that might otherwise confound the results.
Matched Pairs Design in Behavioral Studies
In behavioral research, matched pairs design allows researchers to study the effects of various interventions or conditions while controlling for individual differences. For example, in psychological experiments, participants might be matched based on personality traits, cognitive abilities, or behavioral characteristics. This ensures that the groups being compared are similar, and any observed differences can be attributed to the experimental manipulation rather than individual differences.
Matched pairs design has been used in a variety of psychological studies, from assessing the effects of therapy on mental health outcomes to evaluating the impact of social interventions. By carefully matching participants on key factors, researchers can draw more valid conclusions about the effectiveness of different treatments or interventions.
Business and Marketing Applications
Matched pairs design is also valuable in business and marketing research, particularly for testing consumer preferences or evaluating product changes. In A/B testing, for instance, businesses might use matched pairs design to compare the effectiveness of two different marketing strategies. Customers who are similar in demographic characteristics, such as age and income, can be paired and exposed to different marketing materials. This ensures that any differences in purchasing behavior are due to the marketing strategy, rather than other external factors.
In product testing, matched pairs design can help businesses assess consumer preferences by comparing pairs of consumers who have similar tastes and preferences. This design allows companies to more accurately gauge the impact of product features or changes on consumer satisfaction.
Statistical Analysis in Matched Pairs Design
Paired t-test and Other Statistical Methods
One of the key advantages of matched pairs design is the ability to use powerful statistical tests, such as the paired t-test, to analyze the data. The paired t-test compares the means of the two related groups (treatment and control) to determine if there is a statistically significant difference between them. This test is particularly useful in matched pairs studies because it accounts for the inherent similarity between the pairs, ensuring that any differences in outcomes are not due to random chance.
In addition to the paired t-test, other statistical methods, such as the Wilcoxon signed-rank test, can also be used to analyze matched pairs data. These non-parametric tests are often used when the data do not meet the assumptions of normality required for a paired t-test. Researchers must choose the appropriate statistical method based on the nature of their data and the research question.
Challenges in Analyzing Matched Pairs Data
While matched pairs design offers many advantages, it also presents challenges in data analysis. One common issue is missing data, which can occur if participants drop out of the study or fail to complete certain measures. Handling missing data is crucial, as it can lead to biased results if not properly addressed. Strategies like imputation or complete case analysis can be used to handle missing data, depending on the severity of the problem.
Another challenge is ensuring that the pairs are properly matched. If participants are not adequately matched, the results of the study may be skewed, leading to invalid conclusions. Researchers must carefully select matching criteria and ensure that the pairs are as similar as possible on relevant factors.
Interpreting Results and Drawing Conclusions
Once the data have been analyzed, researchers must interpret the results and draw conclusions. In matched pairs studies, the key focus is on the differences between the treatment and control groups within each pair. A statistically significant difference indicates that the treatment had an effect, but researchers must also consider the size of the effect and its practical significance. In some cases, even small differences can be meaningful, especially in medical or behavioral research where the impact of an intervention may be subtle but important.
Best Practices for Implementing Matched Pairs Design
Selecting Proper Matching Criteria
Choosing the right criteria for matching is crucial to the success of a matched pairs design. Researchers must consider which factors are most relevant to the research question and ensure that they select characteristics that will effectively control for confounding variables. In clinical trials, for instance, matching on age, gender, and baseline health status might be appropriate. However, in educational research, matching on prior academic performance may be more relevant.
It is also essential to avoid over-matching, where too many variables are used to create the pairs. Over-matching can reduce the sample size and increase the risk of bias. Researchers must strike a balance between selecting meaningful matching variables and maintaining a sufficiently large sample size to ensure statistical power.
Ensuring Statistical Power
To ensure that a matched pairs study is statistically powerful, researchers must calculate the necessary sample size based on expected effect sizes and desired confidence levels. Power analysis is a key tool for determining how many participants are needed to detect a meaningful effect. Without adequate statistical power, a study may fail to detect true effects, leading to misleading or inconclusive results.
Researchers should also consider the variability within the matched pairs when determining sample size. If the variability between participants in each pair is large, a larger sample size may be required to detect significant differences.
Handling Bias and Limitations
Like any research design, matched pairs design is not without limitations. Bias can still occur if the matching process is not carefully executed, or if there are unaccounted for confounding variables. Researchers must be diligent in selecting matching criteria and ensuring that the pairs are as comparable as possible.
Additionally, while matched pairs design helps control for individual differences, it cannot eliminate all sources of bias. Researchers must carefully consider the limitations of their study and report them transparently to ensure that their conclusions are grounded in a realistic understanding of the research’s scope and applicability.
Conclusion: Matched pairs design
Matched pairs design is a powerful tool in experimental research that allows researchers to control for confounding variables and increase the precision of their findings. By carefully pairing participants based on relevant characteristics, researchers can ensure more reliable and valid comparisons between treatment and control groups. The design is widely applicable across fields like medical research, education, psychology, and business, making it an essential technique for studies where random assignment is not possible or desirable.
By understanding the key concepts, applications, and statistical methods associated with matched pairs design, researchers can make more informed decisions about when and how to use this methodology in their work. Whether assessing the effectiveness of a new drug, comparing teaching strategies, or testing consumer preferences, matched pairs design offers a rigorous approach to research that yields meaningful, actionable results.

